¿QUE SON LOS PARALELOGRAMOS?

PARALELOGRAMOS

Con origen en el vocablo latino parallelogrammus, el concepto de paralelogramo sirve para identificar a un cuadrilátero donde los lados opuestos resultan paralelos entre sí. Esta figura geométrica constituye, por lo tanto, un polígono que se compone de 4 lados donde hay dos casos de lados paralelos.

Resulta interesante tener en cuenta que existen distintos tipos de paralelogramos. Los paralelogramos del grupo de los rectángulos, por ejemplo, son las figuras donde se pueden advertir ángulos internos de 90º. Dentro de este conjunto están incluidos el cuadrado (donde todos los lados poseen la misma longitud) y el rectángulo (donde los lados que se oponen entre sí poseen longitud idéntica).

Los paralelogramos que se consideran como no rectángulos, por otra parte, se caracterizan por tener 2 ángulos interiores agudos y los restantes, obtusos. Esta clasificación incluye al rombo (cuyos lados comparten una misma longitud y además cuenta con 2 pares de ángulos idénticos) y al romboide (con los lados que se oponen de longitud idéntica y 2 pares de ángulos que también son iguales entre sí).

Para calcular el perímetro de los paralelogramos se necesita sumar la longitud de todos sus lados. Esto puede realizarse a través de la siguiente formula: Lado A x 2 + Lado B x 2. Por ejemplo: el perímetro de un paralelogramo rectángulo que tenga dos lados opuestos de 5 centímetros y otros dos lados opuestos de 10 centímetros, se obtendrá ubicando dichos valores en la ecuación antes planteada, lo que nos dará 5 x 2 + 10 x 2 = 30 centímetros.

Otra fórmula para establecer el perímetro de un paralelogramo es 2 x (Lado A + Lado B). En nuestro ejemplo: 2 x (5 + 10) = 30. Todas estas fórmulas simplifican, en definitiva, el proceso de sumar los lados que posee cada paralelogramo. Si realizamos la operación Lado A + Lado A + Lado B + Lado B, el resultado sería el mismo (5 + 5 +10 + 10 = 30).

La llamada ley del paralelogramo, por otro lado, define que si se suman las longitudes elevadas al cuadrado de cada uno de los cuatro lados de un paralelogramo cualquiera, el resultado que obtendremos será equivalente a sumar los cuadrados de sus dos diagonales.

Con respecto a sus propiedades, resulta necesario contemplarlas en grupos, dado que, como se mencionó anteriormente, muchas formas de características diferentes son consideradas paralelogramos. Algunas de las comunes a todos son:

* Todos poseen cuatro lados y cuatro vértices, ya que pertenecen al grupo de los cuadriláteros;

* Sus lados opuestos nunca se cruzan, dado que siempre son paralelos;

* La longitud de los lados opuestos es siempre la misma;

* Sus ángulos opuestos miden lo mismo;

* La suma de dos de sus vértices, siempre que sean contiguos, da 180°, o sea que son suplementarios;

* Los ángulos interiores deben sumar 360°;

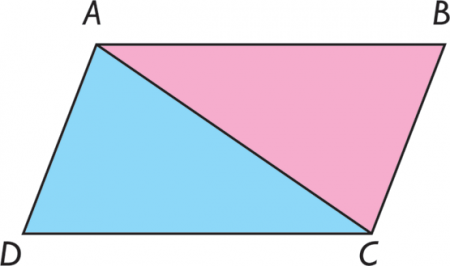
* Su área debe ser siempre el doble de la de un triángulo construido a partir de sus diagonales;

* Todo paralelogramo es convexo;

* Sus diagonales deben bisecarse entre sí;

* El punto en el cual se bisecan sus diagonales es el que se considera el centro del paralelogramo;

* Su centro es a la vez su baricentro;

* Si se traza una recta que cruce su centro el área del paralelogramo se divide en dos partes idénticas.

Por otro lado, los distintos tipos de paralelogramos pueden presentar propiedades particulares, que no se apliquen al resto. Por ejemplo:

* un paralelogramo cuadrado puede dar una figura idéntica si se lo rota en tramos de 90°, lo cual también se puede expresar diciendo que posee simetría de rotación de orden 4;

* Los de tipo romboide, rombo y rectángulo, en cambio, deben ser rotados de a 180° para obtener el mismo resultado;

* un rombo posee 2 ejes de simetría, que lo cortan uniendo sus vértices opuestos;

* un rectángulo, en cambio, tiene 2 ejes de simetría de reflexión que son perpendiculares a sus lados;

* El cuadrado, finalmente, posee 4 ejes de simetría de reflexión, que unen cada par de vértices opuestos y que lo cortan por el centro vertical y horizontalmente.